本次特别分享的是由吉林大学、先进船舶发动机技术全国重点实验室、中国船舶集团有限公司第七一一研究所投稿的“基于数据驱动的柴油发动机部分预混合燃烧模型建模方法”的用户论文。该论文已被2024年度艾迪捷CAE&MBD仿真用户大会收录,荣获“优秀论文”,分享已获得作者的授权。
摘要
部分预混合燃烧(Partially premixed combustion,PPC)作为发动机的一种先进燃烧方式,相比于传统柴油机,能够有效提高热效率,降低碳烟和氮氧化物的排放。PPC主要采用低活性燃料延长滞燃期,利用高压缩比实现预混合气压燃,通过多次喷射策略更灵活地优化燃烧过程。然而,柴油发动机PPC模型具有高度的非线性,其模型参数的确定通常需要耗费大量的人力和物力,且所建立的模型与实际燃烧过程普遍存在较大差异。针对这些问题,本研究将PPC燃烧模型建立为主模型与偏差模型两部分;主模型基于单韦伯方程进行描述,偏差模型则基于在线的高斯过程(Gaussian Process, GP)回归拟合,从而有效降低了传统方法下确定模型参数的工作量,并实现更精确的PPC燃烧模型预测。最后,在GT-SUITE搭建的四缸发动机模型中进行实验验证,采用高斯过程拟合后的缸压均方根误差小于0.14。
关键词
PPC发动机;韦伯方程;高斯过程;模型预测;GT-SUITE
1.引言
由于全球运输贸易的迅猛增速,海上货物运输重要性更加显著[1]。高可靠性、低油耗、广应用范围使柴油机在全世界船用柴油机的市场上拥有头部地位,全世界有80%以上船舶以柴油机作为动力的源头[2,3]。PPC发动机通过部分预混合燃烧过程优化了燃料与空气的混合程度,使得燃烧更均匀和稳定。均匀的燃烧减少了热损失,提高了燃烧效率,也降低了氮氧化物(NOx)和颗粒物(PM)的排放量[4]。此外,PPC发动机通过优化燃油喷射时刻和混合气形成过程,可以避免传统压燃发动机中燃烧过快或燃烧不均匀的问题,降低燃烧过程中的爆震风险。
内燃机的燃烧过程是一个复杂的物理与化学过程,通过详细的化学反应动力学机理建立的模型不利于控制。因此,在满足实时性需求的前提下,为保证对燃烧参数的准确预测,一般采用零维模型和一维模型拟合柴油机的燃烧过程。文献[5]为建立能响应多次喷射的燃烧模型,通过改进柴油机工作过程模型和零维燃烧模型,提出了一种基于零维燃烧模型的二冲程低速船用柴油机性能仿真模型。但该方法主要建立了关于燃油速率的模型,不便用于燃烧过程控制。文献[6]等人对燃烧过程中低温、中温、高温反应进行了现象学描述,并以此建立了零维模型,实验验证显示,该模型具有很好的预测性能。
韦伯燃烧模型作为典型的零维燃烧模型,可以通过调整适当的参数,准确拟合实际的燃烧放热率曲线。因此,利用各种方法识别和优化韦伯方程的参数,以更好地拟合燃烧过程,是内燃机研究的一大热门方向。文献[7]采用偏最小二乘回归将Wiebe参数与运行工况联系起来,可以有效避免单纯使用非线性最小二乘拟合导致的不可能解或多重解。文献[8]提出了基于免疫粒子群优化算法的双韦伯方程标定方法,对25%负荷和100%负荷的放热量分别进行标定,结果表明,量纲为1的决定系数R2大于0.998,最优解稳定性可以达到0.7以上。文献[9]采用神经网络与韦伯燃烧模型相结合,利用神经网络强大的非线性映射能力对双韦伯燃烧参数预测。哈尔滨工程大学胡松[10]等人建立了基于三Wiebe的增压柴油机燃烧模型,并且考虑了柴油机5个运行参数,即转速、进气压力和进气温度、喷油始点以及循环喷油量对9个Wiebe模型参数产生的影响,并提出零维燃烧模型的自动标定算法,对Wiebe燃烧规则的函数以及燃烧参数进行校准,提高燃烧模型的仿真精度。
上述方法的韦伯参数标定通常需要耗费大量的人力和物力,同时实际系统与所建立的模型普遍存在差异。针对这些问题,本研究将PPC燃烧模型的建立分为主模型与偏差模型两部分,主模型基于韦伯方程进行描述,而偏差模型则基于在线学习的高斯过程进行拟合,从而有效降低了传统方法下确定模型参数的工作量,并实现更精确的PPC燃烧模型预测。最终在GT-SUITE四缸发动机模型中进行验证。
2.PPC燃烧过程建模
在以往工作中,对PPC燃烧模型一般采用双韦伯方程或者三韦伯方程来获取更好的拟合效果,但也难以描述传热损失及其他干扰的影响,而且待拟定的参数也会大大增加。本研究将燃烧动态分为主模型与偏差模型两部分。偏差模型依据真实系统数据进行自主学习,从而构建主模型与真实动态的偏差。因此针对主模型可以选择更为简单的单韦伯方程,根据单韦伯方程来建立放热率模型,再通过反推热力学第一定律得到缸压模型。
1
放热率模型

2
缸压模型

3.基于GP的偏差模型
高斯过程是一种对输入数据的函数进行概率建模的方式,可认为是无限多个多元高斯联合分布,其能够结合数据的先验知识,对数据做出预测。本文通过在线收集缸压数据,利用GP来学习主模型与实际缸压之间的偏差,从而对上文韦伯方程建立的缸压模型误差进行补偿,实现燃烧过程的精确预测。
1
数据采集

2
超参数优化

3
高斯回归预测偏差

4.仿真实验验证
在GT-SUITE中搭建四缸发动机仿真模型进行实验验证,仿真模型如图1所示。发动机具体参数如表1所示。为了验证基于GP的补偿模型对不同精度主模型下的适应性,本文分别对主模型有较小误差和较大误差时进行模型验证,模型误差来源于参数的选取和难以精确建模的部分,因此本文通过调节燃烧参数来实现主模型误差大小的调节。
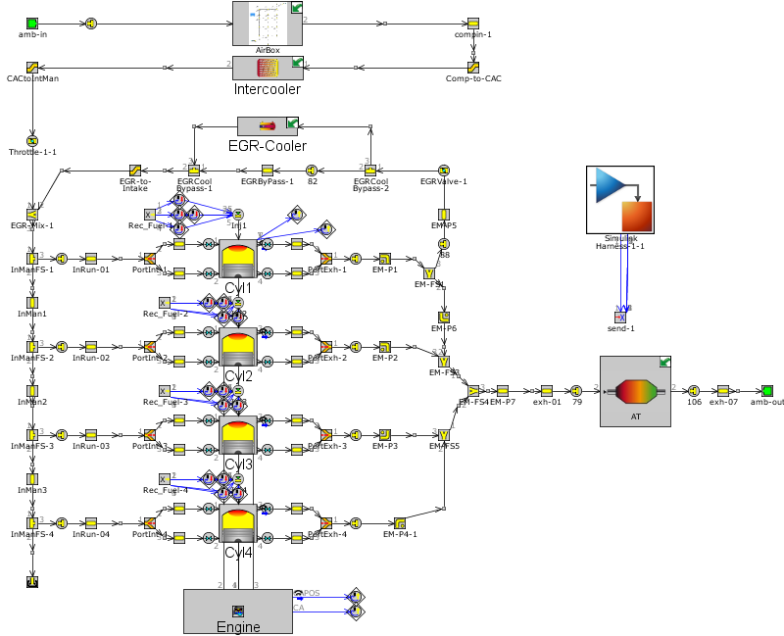
图1 四缸发动机仿真模型
表1 发动机参数
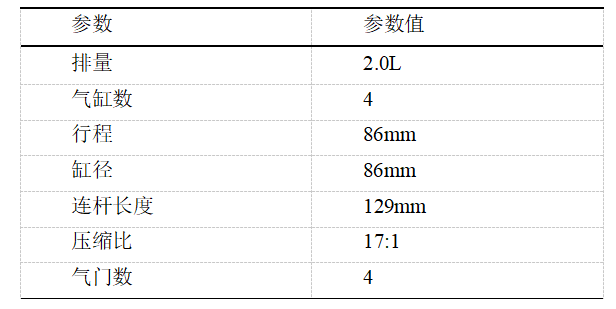
1
主模型有较小误差时的补偿模型验证
通过试验分析燃烧过程缸压及放热量等,调节燃烧参数使得主模型有较小误差,在转速为800rad/min时,分别设置第一次喷油时刻、第二次喷油时刻、第一次喷油量、第二次喷油量初始值为-15、-7、8mg和15mg,在4.5s时第一次喷油量由8mg减到3mg,第一次喷油量由15mg减到10mg,在9.0s时第一次喷油量由3mg增加到13mg。整体缸压如图2(a)所示。
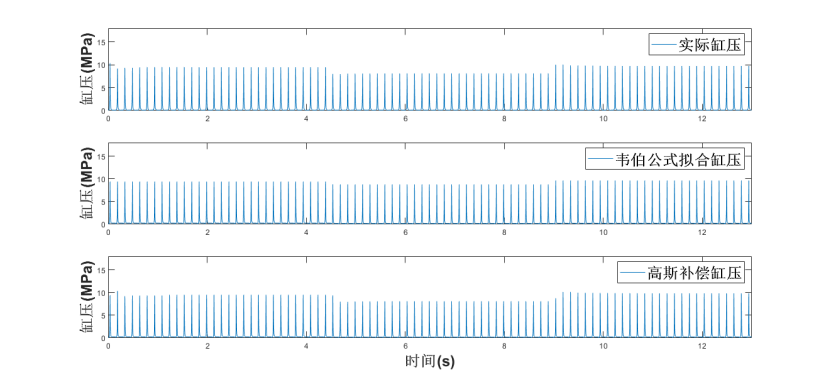
(a)整体缸压图
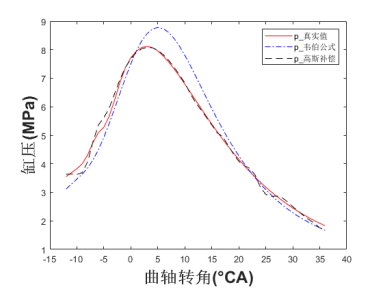
(b)第一次输入量改变缸压稳定后
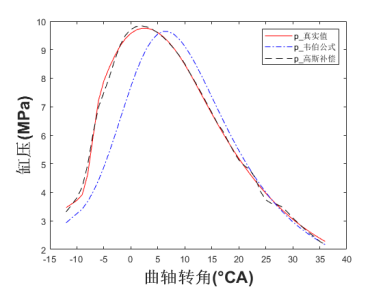
(c)第二次输入量改变缸压稳定后
图2 主模型小偏差模型验证
在4.5s时第一次喷油量由8mg减到3mg,第一次喷油量由15mg减到10mg后,判断每一个工作循环的高斯拟合缸压误差的RMSE是否大于0.04,大于0.04则更新训练数据集,优化超参数。实际缸压稳定后,效果图如图2(b)所示。红色实线表示实际缸压,蓝色点划线为应用韦伯方程和热力学第一定律拟合的缸压,黑色虚线为通过高斯过程补偿的燃烧过程缸压。图2(a)中用韦伯方程拟合的缸压与真实值的RMSE为0.50,最大差值为0.61MPa,用高斯过程补偿后的缸压与真实值的RMSE为0.13,最大差值为0.31MPa。
在9.0s时第一次喷油量由3mg增加到13mg,实际缸压稳定后,效果图如图2(c)所示,用韦伯方程拟合的缸压与真实值的RMSE为1.13,最大差值为3.02MPa,用高斯过程补偿后的缸压与真实值的RMSE为0.13,最大差值为0.41MPa。
2
主模型有较大误差时的补偿模型验证
通过调节燃烧参数使得主模型有较大误差,实验设置同4.1节。整体缸压如图3(a)所示。在4.5s时第一次喷油量由8mg减到3mg,第一次喷油量由15mg减到10mg,实际缸压稳定后,效果图如图3(b)所示。其中,用韦伯方程拟合的缸压与真实值的RMSE为1.2,最大差值为0.85MPa,用高斯过程补偿后的缸压与真实值的RMSE为0.16,最大差值为0.38MPa。在9.0s时第一次喷油量由3mg增加到13mg,实际缸压稳定后,效果图如图3(c)所示,用韦伯方程拟合的缸压与真实值的RMSE为1.56,最大差值为2.68MPa,用高斯过程补偿后的缸压与真实值的RMSE为0.14,最大差值为0.40MPa。
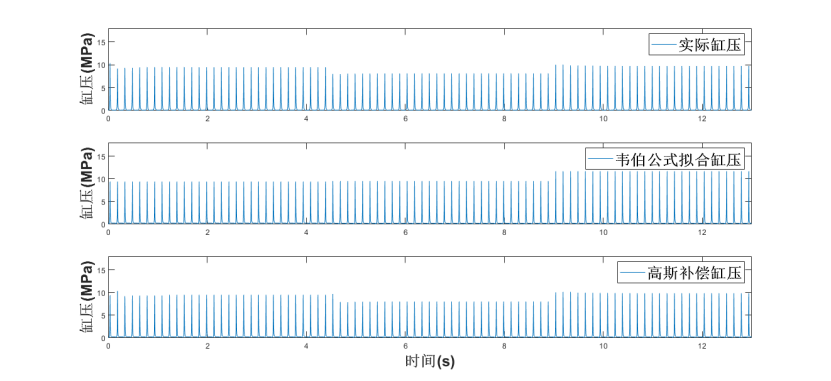
(a)整体缸压图
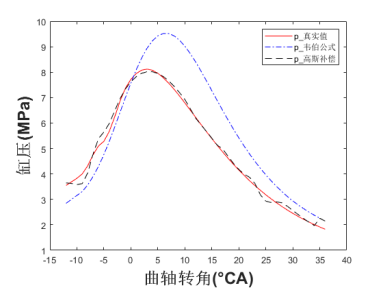
(b)第一次输入量改变缸压稳定后
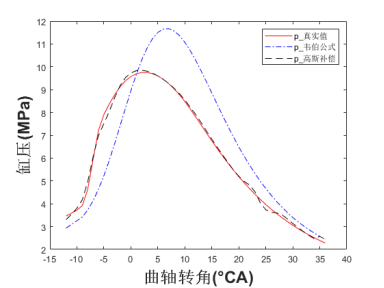
(c)第二次输入量改变缸压稳定后
图3 主模型大偏差模型验证
5.结论
本文基于高斯过程补偿缸压误差进而实现燃烧过程的预测。从实验中可以看出,无论主模型误差大小,采用高斯过程补偿后,模型预测缸压的RMSE值都远小于基于韦伯方程和热力学第一定律所建立的主模型;这意味着应用高斯过程补偿也在保证预测精度的同时,有效降低传统方法下确定模型参数的工作量。同时,在燃烧过程中利用补偿模型得到更准确的缸压动态,对后续发动机PPC燃烧控制提供了更精确的模型保证。
参考文献
[1]. 丁淑富, 孙笋升, 冯细文. 我国船用大功率柴油机产业现状及发展趋势分析[J].柴油机, 2012, 34(05): 1-5.
[2]. 张南林. 舰船柴油机技术现状及发展趋势[J]. 舰船科学技术, 2010 (1): 17-21.
[3]. 罗正刚, 王浒, 尧命发. 大缸径低速二冲程船用柴油机喷油参数的仿真及优化[J].燃烧科学与技术, 2020, 26(06): 535-543.
[4]. 杨添淏.基于模型的部分预混合燃烧发动机控制研究[D].大连理工大学,2020.
[5]. 王海燕,张旭升,胡以怀.基于零维燃烧模型的二冲程船用柴油机性能预测[J].内燃机学报,2016,34(06):549-555.
[6]. Blomberg, Christopher Kim, Yuri Martin Wright, and Konstantinos Boulouchos. "A phenomenological HCCI combustion model in 0D and 3D-CFD." Fuel 226 (2018): 365-380.
[7]. Sun, Yongrui, et al. "Development and validation of a marine sequential turbocharging diesel engine combustion model based on double Wiebe function and partial least squares method." Energy Conversion and Management 151 (2017): 481-495.
[8]. 史明伟,王贺春,杨传雷,等.基于IMPSO的双韦伯燃烧参数标定及预测[J].内燃机学报,2023,41(01):61-67.
[9]. 周峰,刘敬平,阳焱屏,等.多限定参数条件下增压柴油机瞬变过程仿真[J].内燃机工程,2014,35(4):97-102.
[10]. Song Hu,Hechun Wang,Chuanlei Yang,Yinyan Wang. Burnt fraction sensitivity analysis and 0-D modelling of common rail diesel engine using Wiebe function[J]. Applied Thermal Engineering,2017,115.

 B站账号
B站账号

 知乎账号
知乎账号

 微信账号
微信账号